A Solution to LLM Nondeterminism

Much has been made of the problem of hallucinations in large language models (LLMs). The cases of problematic outputs (sometimes hilarious, other times dangerous) are too vast to count—we trust you know of some yourself. Fake legal cases, nonexistent policies, fabricated text, the list goes on.

But hallucinations are, to some extent, just one symptom of a deeper problem in the current approach to LLM inference. That problem? Reproducibility.

It boils down to this: When you prompt an LLM multiple times, the output can vary each time, even if you use the exact same prompt and the exact same model, and even if the temperature is set to zero. The output may be only slightly different, but it will be different.

The problem isn't just a scientific fascination—it's important enough that it was the topic of the first blog post published by Thinking Machines, which starts with the following sentence:

“Reproducibility is a bedrock of scientific progress. However, it’s remarkably difficult to get reproducible results out of large language models.”

If Mira Murati's AI startup (valued at $12 billion) is so focused on this issue, it's a sign that we should all pay attention.

Why does the problem of nondeterminism in LLM inference matter?

Reproducibility problems: Benchmarking becomes fuzzy. Two runs of the same model might yield slightly different scores, making it harder to compare systems fairly or to trust published results. In the realm of developing science-based solutions to hard problems, reproducibility is key.

Verification barriers: In scientific or safety-critical contexts, we need determinism to validate whether an answer is correct. If the output shifts unpredictably, verification costs rise and trust erodes.

Scaling limits: As complexity grows, nondeterminism compounds. Research shows reasoning-augmented models collapse in accuracy beyond certain thresholds, partly because inference isn’t stable across runs. You can imagine this leading to problems in agentic systems trying to manage complex multi-modal problems over a long context window, whether it be managing your personal affairs as an assistant or managing a country's power grid.

In consumer-level AI, determinism will matter when it comes to making truly helpful agentic AI products that actually work. In enterprise and mission-critical contexts, determinism is a pre-requisite for incorporating AI into workflows in a productive, safe, and reliable manner.

Understanding the Challenges & Presenting a New Solution

We're excited to announce that we have developed a stable solution for nondeterminism in LLMs.

In this blog, we'll dive into the 3 problems that lead to nondeterminism in LLM inference, take a look at how Thinking Machines has been thinking about the challenge, and outline our solution in detail.

We've included a short demonstration of the tech at work, as well as a link to a free tool to test our solution on your own.

Understanding Variability in LLM Outputs

Temperature is a variable that is designed to introduce variability to an LLM's output. The higher the temperature, the more stochastic variability will manifest in the system output. Hypothetically, setting temperature=0 should remove any variability, or nondeterminism, in the output. But even in the case of temperate=0, LLMs still demonstrate nondeterminism (more on that later).

A tool like ChatGPT will likely have some temperature built in to provide a bit of randomness, which increases the feeling that you are talking to something more intelligent, more human in nature. Here you can see that in action.

In the case above, it's not necessarily a problem to get a different output for the same input. Each output is satisfactory in its own way.

But there are some cases when the output shouldn't vary; for example, in math. 2+2=4, right?

Right! In the case of 2+2, there is only one statistically correct answer, so regardless of the temperature setting, the answer should always be 4. So far so good.

This same logic should then apply to all math for which there is a determined single correct answer. However, here is where we start to see LLMs fail.

Problem #1: Floating-Point Math

The first reason why LLMs don’t necessarily output reliably consistent results is the underlying foundation of most computer software. The problem lies in the use of floating-point mathematical approximation at high data resolution. For most computer programs, this approximation trick is a totally acceptable way to get really fast code.

Floating-point math speeds up computations a lot, but creates small inaccuracies by destroying information along the way. Thinking Machines outlines this part of the problem clearly in this section of their blog post.

Needless to say, if information is destroyed along the way, then as complexity increases (something we observe in recursive agentic AI systems), the more these small inaccuracies contribute to deviation from the intended output.

If a system like ChatGPT writes a piece of code to deliver a result, it may incorporate such inaccuracies into its output. Here's an example:

The answer to the above should be zero. Let's break it down:

1. a-b=100000000-0.01=99,999,999.99
2. 99,999,999.99-100000000=-0.01
3. -.01+0.01=0

The reason the code in the example above gets it wrong? Because it's converting the variables to floating-point:

The expression is evaluated left to right as ((a - b) - a) + b.

Because b = 0.01 isn’t exactly representable in binary and because we subtract two large, almost-equal numbers in the middle, the tiny rounding error from the first subtraction doesn’t cancel out.

What’s left is about −5.3644180296×10⁻⁹.

• a = 100000000.0 is exact in float64.
  Hex: 0x1.7d78400000000p+26
• b = 0.01 is not exact; the stored value is slightly larger:
  Hex: 0x1.47ae147ae147bp-7
  Decimal: 0.010000000000000000208166…

Step-by-step breakdown

t1 = a - b
Exact math wants 99,999,999.99, but at ~1e8 we can only hit multiples of ~1.49e-08.
So we land a bit low by 0.36 ULP:(Unit in the Last Place).

t1 = 99999999.99  (as printed)
t1 = exact(99,999,999.99)
− 5.364418029785156e-09
Hex: 0x1.7d783fff5c28fp+26

t2 = t1 - a
This is the catastrophic-cancellation moment: subtracting two ~1e8 numbers leaves a tiny residue that’s dominated by the rounding from step 1.

t2 = -0.01000000536441803
   = -(b) − 5.364418029785156e-09
Hex: -0x1.47ae200000000p-7

t3 = t2 + b
+ b cancels the -b part of t2, but it can’t cancel the leftover −5.3644…e-09.

t3 = -5.364418029576989e-09
Hex: -0x1.70a3d70a00000p-28

So the final result is the first-step rounding error (≈ −5.3644e-09), nudged by a tiny (~2.08e-19) effect from b being inexact.

Problem #2: Concurrency

When using floating-point math, concurrency at runtime introduces the second problem. For example, if you complete the elements of the equation above in a different order, you will get a different result.

• If you reorder the math as (a - a) + (-b + b), you’d get exactly 0.0 in float64.
• But your original order ((a - b) - a) + b locks in the first rounding error, and the middle cancellation amplifies it.

Thinking Machines explains it this way:
"Typically a GPU launches a program concurrently across many “cores” (i.e. SMs). As the cores have no inherent synchronization among them, this poses a challenge if the cores need to communicate among each other. For example, if all cores must accumulate to the same element, you can use an “atomic add” (sometimes known as a “fetch-and-add”). The atomic add is “nondeterministic” — the order in which the results accumulate is purely dependent on which core finishes first."

Imagine this in a recursive AI system: You give the system a big problem, it breaks the problem down into many subtasks, each with varying types of problems within—some may involve writing code, analyzing images, writing text, etc.

On two subsequent runs, because of the order of operations issue outlined above, you may get completely different results.

This can be amplified even further by the primary culprit identified by Thinking Machines: batch invariance.

Problem #3: Batch Invariance

In addition to floating + concurrency, challenges, Thinking Machines identifies a deeper problem: “The primary reason nearly all LLM inference endpoints are nondeterministic is that the load (and thus batch-size) nondeterministically varies!”

Thinking Machines' Solution to Batch Invariance (in a Nutshell)

• Their fix: make every reduction batch-invariant
• They rework the three reduction hotspots (RMSNorm, Matmul, Attention) so the reduction order is independent of batch size/position

Thinking Machines notes that while they are able to achieve stable nondeterminism with their solution, it entails a 60% slowdown versus typical methods, and it only works on a GPU (get all the details on their approach here).

We have developed another approach that solves for all three problems that contribute to nondeterminism, can run on a GPU or a standalone consumer device (e.g., a Mac Studio), and does it with only a 5-20% slowdown.

Our Solution to Nondeterminism in LLM Inference

Back in 2020, our team began laying the groundwork for our core technology: A proprietary framework enabling the functional application of dynamic multi-agent AI. In order to actually work, our framework needed to address the issue of nondeterminism.

Our system solves each component of the problems outlined above and can reliably output the exact same results with temperature set to zero.

How we solve the floating-point problem

Instead of floats, we use long math (integer/fixed-point) to eliminate non-associativity. Every floating-point variable is represented as a set of integers, the same as how humans do calculations with any numbers. Normally this would be ~40× slower (which is why it isn't used commonly), but with our patented FIONa boolean-to-math conversion (US11029920B1), we cut it to just a 5–20% slowdown.

This technology is also at the root of our solutions to the next two problems.

How we solve the concurrency problem

With branchless integer arithmetic, concurrency doesn’t introduce nondeterminism. Every core executes the same deterministic operations; no race conditions from float accumulation.

How we solve the batch invariance problem

Our arithmetic kernels are designed to be inherently batch-invariant.

• Each sequence is computed independently with deterministic integer reductions.
• Scaling to different batch sizes doesn’t alter the accumulation order or the final result.
• This ensures consistent outputs whether you run 1 request or 100 simultaneously.

Watch the Demo

What you'll see in the above demo:

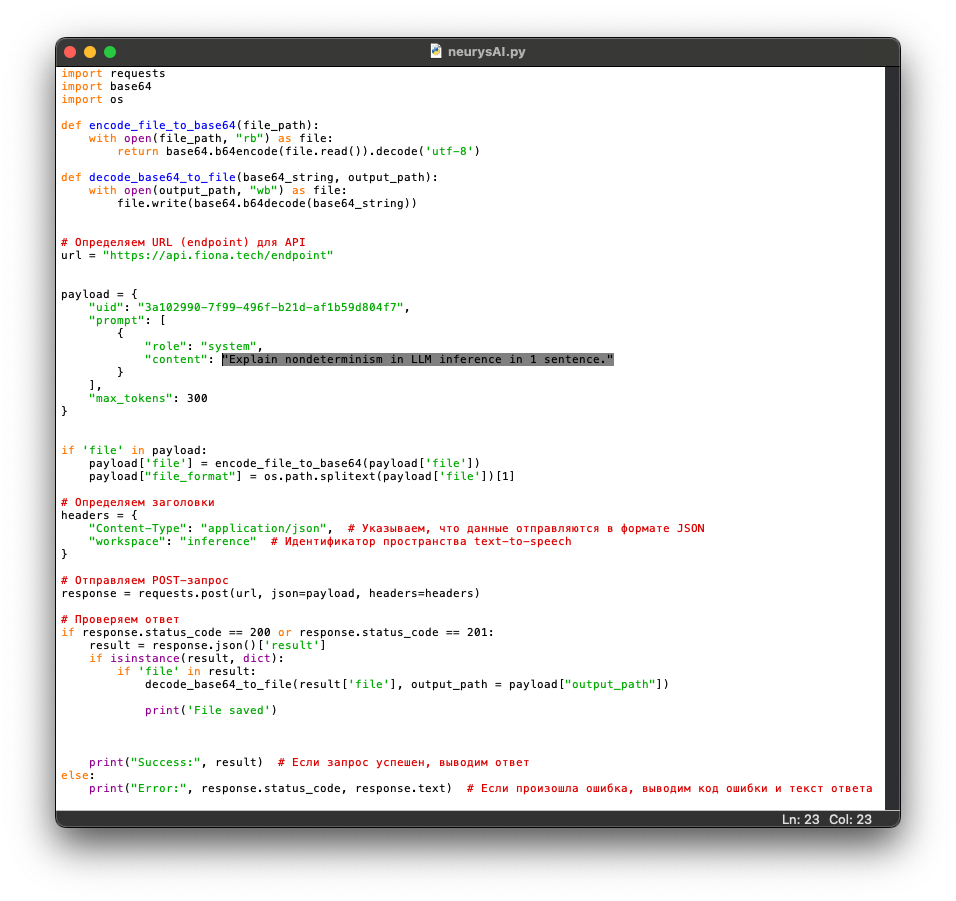
1. We use our iCon Cloud tool to load an open-source LLM (Qwen3-4B-Instruct-2507) into our proprietary Container-Specific Programming Language (CSPL) Interpreter.
2. We select AWS to managing user interfacing and storing the selected model.
3. iCon Cloud provides API code in Python to plug into a project.
4. We see a Python run of the API code, with prompt "Explain nondeterminism in LLM inference in 1 sentence."
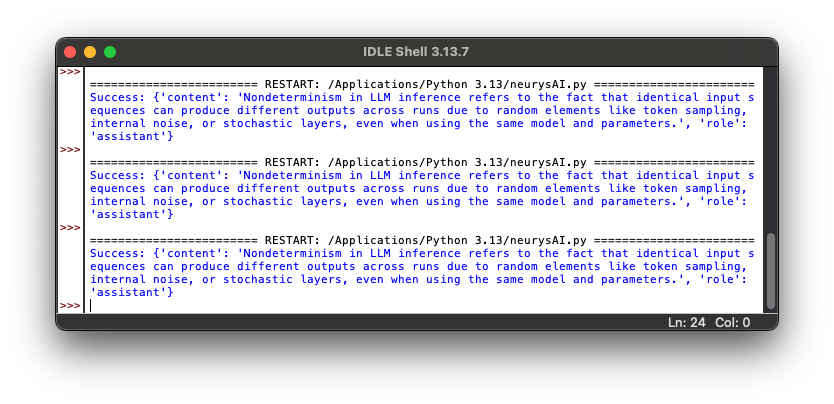
5. Inference is run (using the previously selected LLM) on our proprietary interpreter, which includes our determinism solution in the form of our patented FIONa technology.
6. Inference is run 2 more times, for the same prompt.
7. All three outputs are pasted into Google Sheets, with conditional cell formatting illustrating that all three outputs are indeed exactly the same.

Try Our Solution Yourself

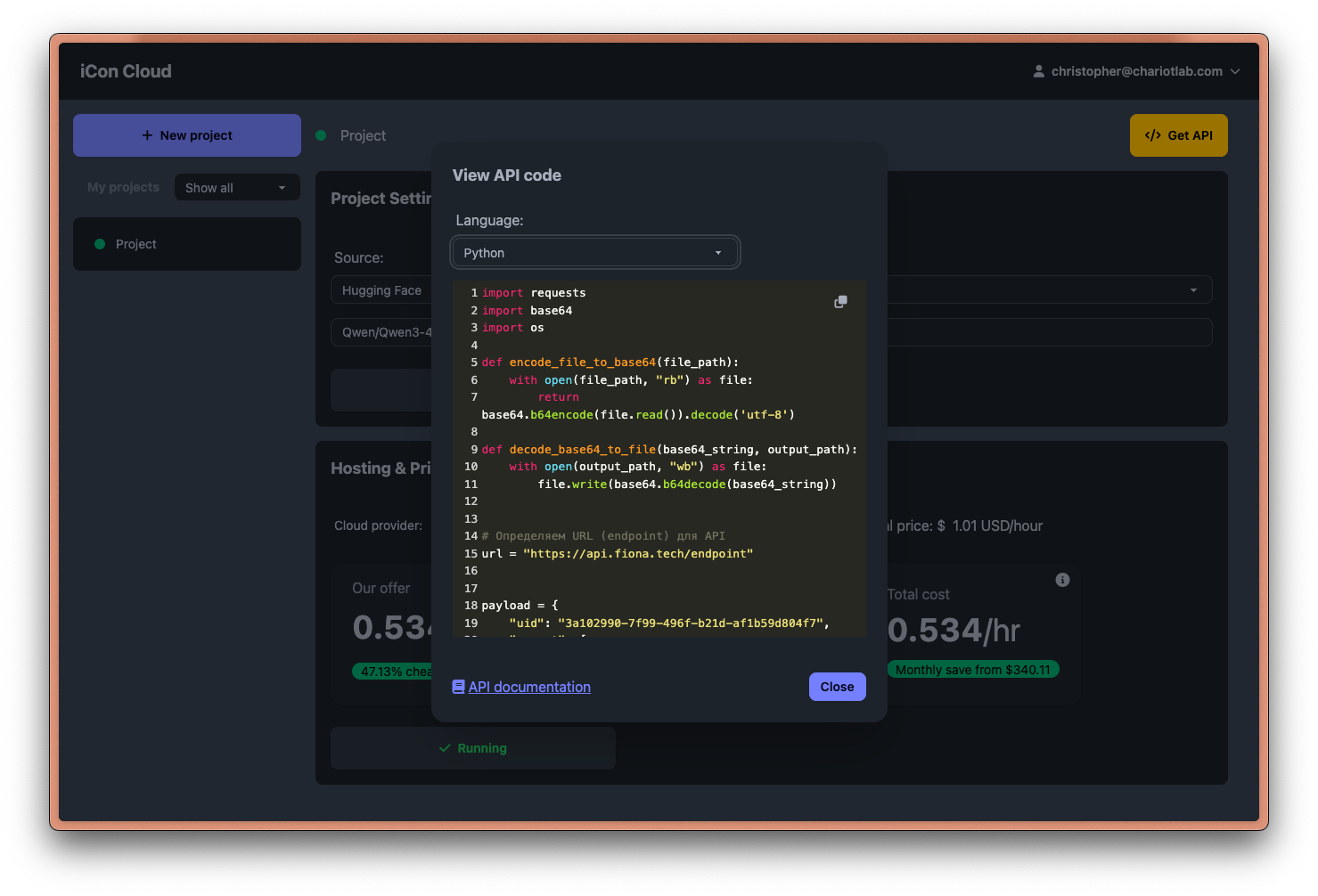
You can use our iCon Cloud service for free to test our determinism solution. Visit iconcloud.ai and register for a free account, then follow the steps shown in the above demo. You can then compare outputs from the same LLM you've chosen, run in a separate environment, with temperature=0. Without running inference on our interpreter, you will observe nondeterminism.

Need assistance? Email us at: [email protected]

Takeaway: A Practical Solution to LLM Nondeterminism Paves the Way for Complex Multi-Agent AI

Thinking Machines came up with a way to reduce nondeterminism, addressing the batch invariance problem specifically. Their result comes with a. 60% slowdown. Our approach addresses all of the challenges that drive nondeterminism, and does so much faster, demonstrating only a ~5-20% slowdown vs. typical inference.

With this at the core of our technology, we can support the development of advanced reasoning AI systems— personal assistants with superior IQ and human-level EQ, enterprise solutions for mission-critical reliability, and robot brain operating systems capable of continual learning and real-time adaptation.

Request our tech paper

If you'd like to review our long-term paper describing our dynamic multi-agent AI system (built on an interpretable containers modular architecture and utilizing our proprietary framework and CSPL Interpreter), please email us at: [email protected]